System liczbowy – zbiór reguł jednolitego zapisu , nazewnictwa i działań na liczbach. Do zapisywania liczb zawsze używa się pewnego skończonego zbioru znaków, zwanych cyframi. Cyfry można zestawiać ze sobą na różne sposoby (według określonych przez dany system reguł) otrzymując nieskończoną liczbę kombinacji. Systemy liczbowe dzielimy najogólniej na: addytywne – systemy w których wartość liczby jest sumą wartości jej znaków cyfrowych. pozycyjne – systemy, w których wartość liczby jest zależna od położenia (pozycji) cyfry w liczbie.
System binarny: System binarny jest najprostszym systemem pozycyjnym. Podstawa p = 2. Do zapisu liczb potrzebne są więc tylko dwie cyfry: 0 i 1. Konwersje z (2) na (10) i odwrotnie odbywają się wg schematu opisanego w punktach 1.3 i 1.4. System jest powszechnie używany w informatyce.
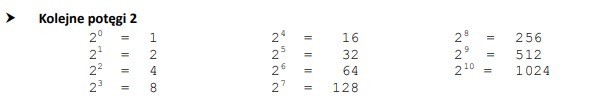
System ósemkowy
Oprócz systemu dwójkowego w informatyce powszechnie są stosowane dwa systemy - ósemkowy (oktalny) oraz szesnastkowy (heksadecymalny). Powodem ich stosowania jest to, iż bardzo łatwo jest przeliczać pomiędzy nimi a systemem dwójkowym. Liczba ósemkowa jest dla ludzi bardziej czytelna od liczby dwójkowej.
W systemie ósemkowym mamy 8 cyfr: 0, 1, 2, 3, 4, 5, 6 i 7. Wartość liczby ósemkowej obliczamy wg wzoru:
W8 = cn-18n-1 + cn-28n-2 + ... + c282 + c18 + c0
ci, i = 0,1,...,n-1 - kolejne cyfry ósemkowe zapisu liczby
Przykład:
72318 = 7 × 83 + 2 × 82 + 3 × 8 + 1
72318 = 7 × 512 + 2 × 64 + 3 × 8 + 1
72318 = 3584 + 128 + 24 + 1
72318 = 3737
Istnieje również inny algorytm obliczania wartości dowolnej liczby pozycyjnej, zwany schematem Hornera. Postępujemy następująco:
Za wynik W przyjmujemy pierwszą od lewej cyfrę liczby. Kolejne cyfry liczby odczytujemy od strony lewej ku prawej.
Dopóki są dalsze cyfry, wynik W mnożymy przez podstawę systemu i dodajemy do niego kolejną cyfrę, aż do ich wyczerpania.
Na końcu W zawiera wartość liczby.
Przykład:
Mamy znaleźć reprezentację liczby 10000 w systemie ósemkowym.
| 10000 | : 8 = | 1250, | reszta 0 |
| 1250 | : 8 = | 156, | reszta 2 |
| 156 | : 8 = | 19, | reszta 4 |
| 19 | : 8 = | 2 | reszta 3 |
| 2 | : 8 = | 0 | reszta 2 |
10000 = 234208
Liczby ósemkowe bardzo prosto przeliczamy na system binarny. Jedna cyfra ósemkowa zawsze przechodzi w trzy cyfry binarne:
| cyfra ósemkowa |
cyfry dwójkowe |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
System dziesiętny
Dla ludzi naturalnym sposobem prezentacji liczb jest system dziesiętny. Oznacza to, że wyróżniamy dziesięć cytr. Są nimi: zero, jeden, dwa, trzy, cztery, pięć, sześć, siedem, osiem oraz dziewięć. Oznacza się je odpowiednio: 0, 1, 2, 3, 4, 5, 6, 7, 8 oraz 9. Wliczając zero, jest ich dziesięć. Zapis dziesiętny powstał wieki temu, prawdopodobnie, dlatego, że mamy dziesięć palców.
Umiemy już policzyć do dziecięciu, wliczając liczbę zero. Natomiast co się stanie, gdy będziemy mieli do policzenia jakąś większą ilość? Otóż, przeskakujemy automatycznie, na następną pozycję, a cyfry zwiększmy tylko na pozycji wysuniętej najbardziej w prawo. Właśnie ta najbardziej w prawo wysunięta pozycja jest najsłabsza, a najbardziej w lewo - najmocniejsza. Tym sposobem znowu zwiększamy cyfry, aż uzyskamy dziewięć. Następna liczba, przesunie cyfrę, która znajduje się o jedną pozycję w lewo. Natomiast gdy już nawet dziewiątka będzie na najbardziej w lewo wysuniętej pozycji, dodajemy nową pozycję. Cykl zaczyna się ponownie i tak w nieskończoność. Zobaczmy na przykładzie.
Weźmy na przykład liczbę 274, czyli dwieście siedemdziesiąt cztery. Na najsłabszej pozycji widnieje cyfra 4. Pozycja ta nosi nazwę pozycji jedności, jeśli pamiętacie ze szkoły podstawowej. Mamy zatem 4 jedności. Na drugiej pozycji jest cyfra 7. Cyfra ta znajduje się na drugiej pozycji, czyli pozycji dziesiątek. Można więc powiedzieć, że jest tam siedem dziesiątek, inaczej mówiąc 70 jedności. Na trzeciej natomiast pozycji jest cyfra 2. Trzecia pozycja to pozycja setek, czyli mam dwie setki. Innymi słowy, liczba 274 to dwie setki, siedem dziesiątek i 4 jedności. Można to zapisać następująco: 4*1 + 7*10 + 2*100. Po dokonaniu tegoż działania, wyjdzie 274. Jak widać, każdy kolejny składnik zawiera cyfrę z powyższej liczby oraz ciągle zwiększający mnożnik. Mnożnik ten najpierw jest równy 1, potem 10, a na końcu 100. Znaczy to, że każdy następny jest pomnożony przez 10.
Można więc zapisać to jeszcze inaczej. Liczba 274 to tak jak: 4*100 + 7*101 + 2*102 . Jak widzimy, mnożnik to liczba 10 z ciągle zwiększającą się potęgą.
SPRÓBUJ SAM!
Zapisz liczbę dziesiętną będącą rokiem Twojego urodzenia z wykorzystaniem kolejnych potęg liczby dziesięć.
Zapisz liczbę 1456(10) z wykorzystaniem kolejnych potęg liczby dziesięć.
System szesnastkowy
czyli heksadecymalny https://pl.wikipedia.org/wiki/Szesnastkowy_system_liczbowy
Znamy już 2 systemy liczbowe: dziesiętny i dwójkowy. Wszystkie one działają analogicznie tak samo, zmienia się tylko podstawa, czyli ilość cyfr. Teraz zajmiemy się nieco systemem szesnastkowym inaczej zwanym heksadecymalnym. Jest on dość szeroko stosowany w dzisiejszej informatyce. Podstawą tego systemu jest 16. Musi istnieć więc szesnaście cyfr. Pierwsze dziesięć już znasz. Są nimi odpowiednio: 0, 1, 2, 3, 4, 5, 6, 7, 8 oraz 9. W naszym systemie, kolejną liczbą jest 10, natomiast w systemie szesnastkowym jest ono reprezentowane przez A. Kolejne liczby to: 11 - B, 12 - C, 13 - D, 14 - E, 15 - F. Zatem, np. liczby w systemie dziesiętnym: 2, 6, 9, 11, 14, w systemie szesnastkowym wyglądają odpowiednio: 2, 6, 9, B, E. Widać od razu, że duże liczby zajmują w systemie szesnastkowym mało miejsca. Dlatego właśnie jest on tak przydatny.
Konwersja liczby szesnastkowej na dziesiętną
Konwersja ta odbywa się podobnie jak w przypadku liczb binarnych, z tym, że podstawą jest nie 2 a 16. Weźmy dowolnie wymyśloną liczbę w zapisie szesnastkowym, na przykład AB12 (co czytamy: a b jeden dwa). Bierzemy cyfrę wysuniętą najbardziej w prawo i postępujemy tak samo jak w przypadku liczb dwójkowych, ale zamiast mnożnika 2 mamy 16. Zatem jest to: 2*160 + 1*161 + 11*162 + 10*163 , a więc jest to 2 + 16 + 2816 + 40960, a więc jest to liczba 43794 w zapisie dziesiętnym.
Konwersja liczby dziesiętnej na szesnastkowy
No to warto by było teraz z powrotem odwrócić liczbę 43794 w zapisie dziesiętnym na AB12 w szesnastkowym. Najpierw musimy sobie napisać jakie są kolejne wielokrotności liczby 16. A są to: 1, 16, 256, 4096, 65536 itd. Jak widać nasza liczba w systemie dziesiętnym, czyli 43794 jest między liczbą 4096, a 65536. Bierzemy pod uwagę liczbę mniejszą od naszej, czyli 4096. Jest ona czwartą wielokrotnością, więc nasza liczba w systemie szesnastkowym będzie miała 4 cyfry (na razie wszystko się zgadza). Teraz sprawdzam, ile razy liczba 4096 mieści się w naszej liczbie konwertowanej, czyli 43794. Okazuje się, że mieści się 10 razy. 10 w systemie szesnastkowym to A, zatem pierwsza cyfra to A. Jak widać, w dalszym ciągu wszystko się zgadza. Teraz, skoro liczba 4096 zmieściła się dziesięć razy w 43794, to jeszcze zapewne została jakaś reszta. Obliczamy sobie tą resztę. Mnożymy zatem 4096*10 co daje 40960. Teraz odejmujemy wynik od naszej liczby i obliczamy resztę. Zatem 43794 - 40960 = 2834. To jest nasza reszta. Następnie z resztą postępujemy tak samo, jak na początku konwersji. Już na oko widać, że w następnym kroku sprawdzamy ile razy 256 mieści się w 2834. Mieści się 11 razy, zatem kolejna cyfra szukanego zapisu to B. Następnie znowu: obliczamy resztę, itd. Końcowy wynik powinien wynosić AB12. Tak oto skonwertowaliśmy liczbę z zapisu dziesiętnego na szesnastkowy.
Konwersja liczby dwójkowej na szesnastkowy
Konwersja ta jest bardzo prosta i wcale nie wymaga skomplikowanych obliczeń. Zobaczcie, jaka jest maksymalna liczba w zapisie dwójkowym składająca się z 4 bitów. Jeżeli liczba ma być maksymalna, wszystkie jej cyfry muszą mieć maksymalne wartości. Ma ona zatem postać: 1111. Po przeliczeniu, otrzymamy 15 w zapisie dziesiętnym. Jak pewnie zauważyliście, 15 jest to maksymalna cyfra w zapisie szesnastkowym, czyli F. Daje to trochę do myślenia, ale najważniejszy jest jeden fakt: każda liczba składająca się z czterech cyfr w zapisie dwójkowym da się zapisać jako jedna cyfra w zapisie szesnastkowym.
Liczby szesnastkowe również jest łatwo przeliczać na liczby dwójkowe. W tym przypadku każda cyfra szesnastkowa zastępuje cztery cyfry binarne - dzięki temu liczby szesnastkowe bardzo dobrze odwzorowują dane 8, 16, 32 bitowe. Tabelka konwersji jest następująca:
|
cyfra |
cyfry |
|
0 |
0000 |
|
1 |
0001 |
|
2 |
0010 |
|
3 |
0011 |
|
4 |
0100 |
|
5 |
0101 |
|
6 |
0110 |
|
7 |
0111 |
|
8 |
1000 |
|
9 |
1001 |
|
A |
1010 |
|
B |
1011 |
|
C |
1100 |
|
D |
1101 |
|
E |
1110 |
|
F |
1111 |
Przeliczanie liczby szesnastkowej na ósemkową polega na zamianie każdej cyfry szesnastkowej grupą 4 cyfr binarnych:
|
AF9D716 → |
A |
F |
9 |
D |
7 |
|
|
|
1010 |
1111 |
1001 |
1101 |
0111 |
→101011111001110101112 |